直角三角形斜边公式怎么算（勾股定理是怎么诞生的？）

勾股定理，是最为国人所熟知的数学定理。光看这定理名称就很特别，极具中国古典气息。

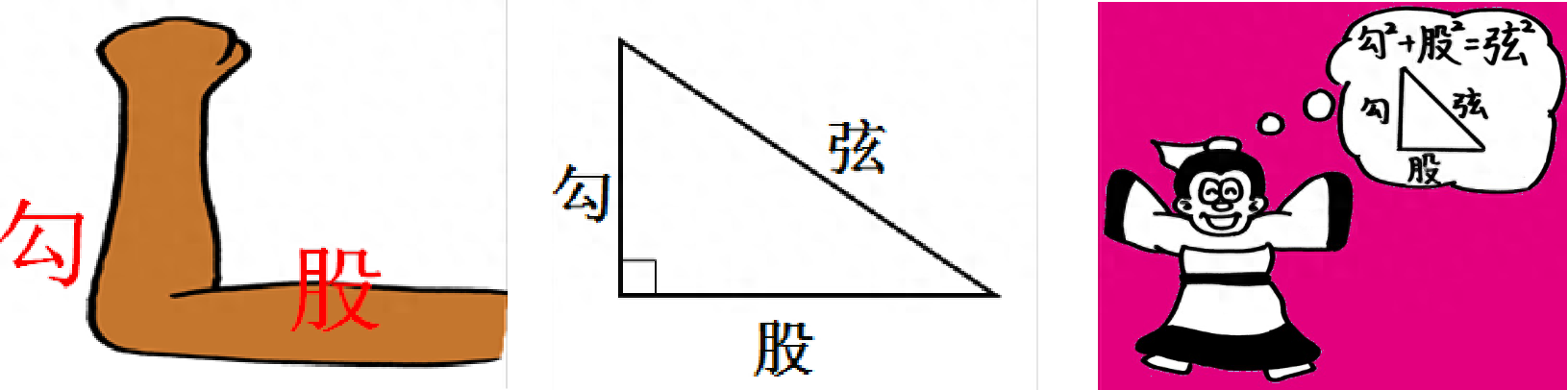
“勾股”是什么意思呢？原来，中国古人把支成直角的手臂，小臂称为“勾”，大臂称为“股”，所以古人就把直角三角形称为“勾股形”；其中直角边中较短的为“勾”，较长的为“股”，斜边为“弦”。勾股定理，是指直角三角形的三个边之间的基本关系，即直角三角形的两条直角边的平方和等于斜边的平方，用公式表示就是：a²+ b² =c² 。

勾股定理有多重要？首先，它是人类早期发现并证明的重要数学定理之一，被誉为“几何学的基石”；其二 ，它是用代数思想解决几何问题的最重要的工具之一；其三，从古至今，它都有着巨大的实用价值。

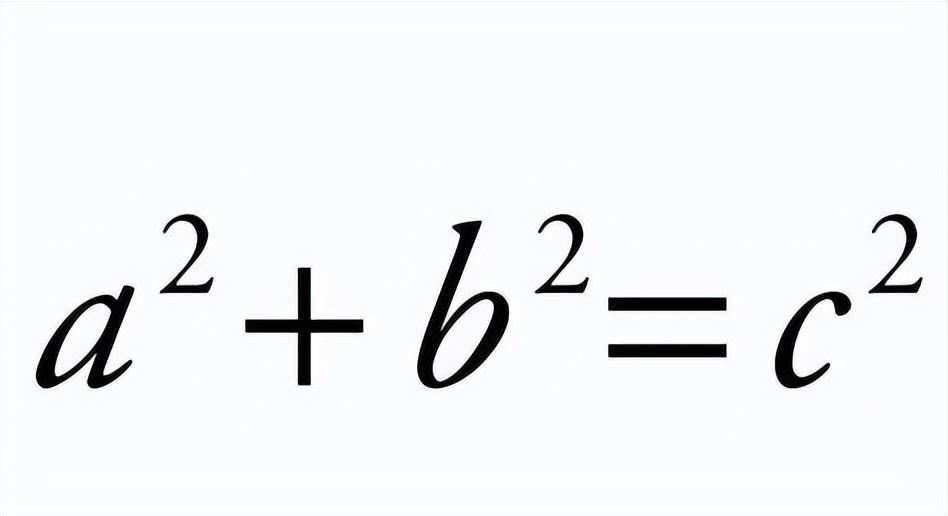
一、中西之争

如此意义重大的勾股定理，它是怎么诞生的呢？这事，一直存在着争议：是西方最早发现的，还是中国最早发现的？近些年来，更有些国人提起勾股定理，只提西方，不提中国，甚至否认中国古人对勾股定理的证明，在此，我们得好好理一理勾股定理的历史。

在西方，相传勾股定理的发现者是古希腊数学家毕达哥拉斯：公元前六世纪的某天，毕达哥拉斯去参加宴会，主人家的方砖地板引发他的兴趣，一番演算之后，他发现了“直角三角形斜边上的正方形，等于两直角边上的两个正方形之和”。为此他和弟子们宰了一百头牛以作庆祝。所以西方将这个发现命名为”毕达哥拉斯定理“，又称”百牛定理“。

但是，毕达哥拉斯的证明方法早已失传了，一直到了公元前三世纪，古希腊数学家欧几里得才在其著作《几何原本》中给出了西方的第一个证明。

而在中国，勾股定理的发现可追溯到公元前十一世纪，比毕达哥拉斯提早了五百多年，对勾股定理的证明更比欧几里得提早了八百多年，最早记载于古书《周髀算经》中。

《周髀算经》原名《周髀》，大约成书于公元前一~二世纪的西汉时期，在唐代被列入《算经十书》，并更名为《周髀算经》。这本古书是中国历史上最早的数学和天文学著作，它在数学方面最重要的价值之一，就是对于勾股定理的介绍与证明，其中最重要的一段记载，是商未周初时期，周公与商高的一段对话——周公问数。

二，勾三股四弦五

周公，名姬旦，是西周的开国元勋，周文王姬昌的第四个儿子；商高是商未周初的数学家。三千多年前的一天，周公向商高提问：“古代伏羲作天文测算和制定历法，但是天那么高却没有阶梯可以攀登，地那么广也不能用尺子去测量，请问天与地的数据是如何得出来的？”

商高回答：“数的法则是根据圆形和正方形得出来的。圆形出自于正方形，正方形出自于曲尺（直角三角尺），矩形的面积是根据乘法计算出来的。折出一个曲尺，短的一边（勾）为三，长的一边（股）为四，对角线（弦）则为五。”

商高这里说的“勾三股四弦五”，即3，4，5，这是一组勾股数，同时代表着勾股数的比例，相于当勾股定理公式中的a、b、c。接着，商高法证明了勾股定理。

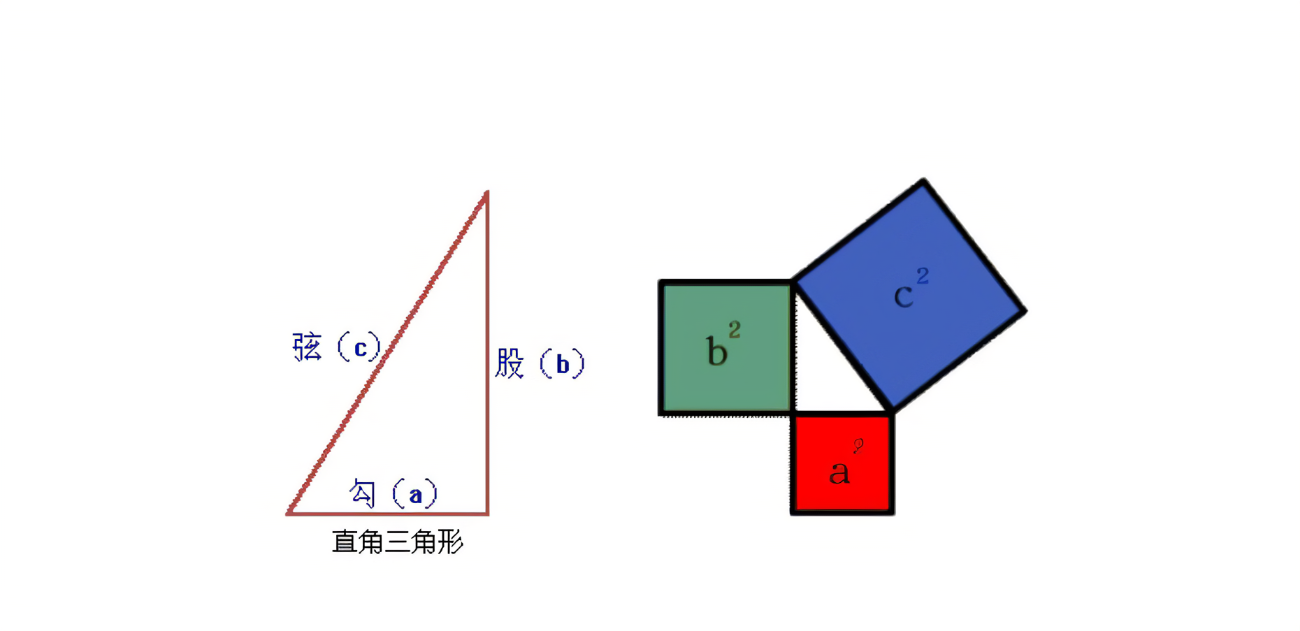
商高说：“选择一个勾为3股为4的曲尺，曲尺两端的连线（弦）必为5。以勾和股为边长，各画成勾方和股勾，再在弦线的外面再画一个三角形，并用这个三角形环绕勾方和股勾，形成一个大正方形，其中有边长为3的勾方、边长为4股方以及边长为5弦方共三个正方形。而勾方和股方的面积之和为25，即是弦方的面积，这叫作积矩。”总结为：勾的平方+股的平方=弦的平方，也就是3²+4²=5²，即：a²+ b² =c²。

这就中国乃至世界第一个被记载并流传下来的勾股定理证法。因此，勾股定理又称“商高定理”。

三、赵爽弦图

可惜《周髀算经》中商高的原文配图失传了。到了三国时期，吴国数学家赵爽在研究《周髀算经》时，对商高的原文作出了“勾股圆方图说”的注释，对勾股定理的表述为：“勾股各自乘，并之（相加），为弦实。开方除之，即弦。”用公式表示：c=√（a²+b²）。

赵爽还创作了“弦图”，用形数结合的方法，更加详细直观地证明了勾股定理。

根据赵爽弦图，可得出公式：4×（ab/2）+(b-a)²=c² ，化简后即是：a²+b²=c²。

赵爽的“勾股圆方说”与“弦图”，是在商高理论基础上，对勾股定理的一个重要证明，是中国古代代数和几何紧密结合、以形证数的一个典范。

四、 勾股定理溯源

《周髀算经》中，商高在证明了勾股定理之后，对周公说：“当年大禹治水时，就已经在使用这个定理。”那么，上古中国人又是如何发现勾股定理的呢？

回顾前文提到的，周公问商高：伏羲是怎么测量出天与地的数据的呢？

伏羲，是中华民族的人文初祖之一，善于思考和发明创造。他观察到，树木、房屋等固定的物体，在太阳光照射下所产生的影子，会随着时间和季节发生变化，并有着一定的规律。据此，伏羲发明了圭表，这是中国最早的测量日影长度的天文仪器。

最初的圭表是在地平面上垂直立起一根木杆子，通过观测木杆正午时影子的长短变化，以确定季节的变化：影子最短是夏至，影子最长是冬至。古人掌握了日影与季节之间的规律，把目光投向更高远的宇宙，探究日月星辰，后来就有了“陈子测日”。

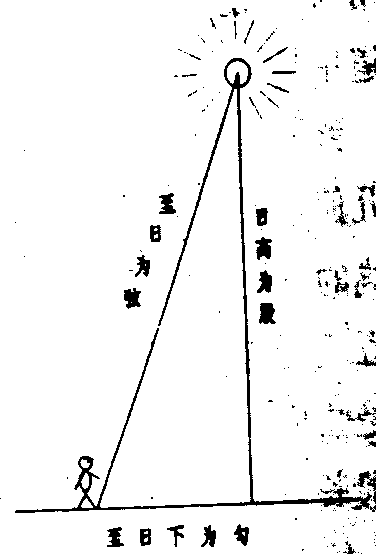
陈子，生活于公元前6~7世纪，是周公的后人，也是一名数学家。《周髀算经》有一段关于他测量太阳有多远的记载，其计算方法是：将勾（观察点到太阳正下方的距离）、股（太阳到地面的垂直距离）各自平方后相加，再开方，就得到弦（观察点到太阳的距离），用当代公式表示即是：c=√（a²+b²）。

由于古代科学水平的限制，陈子认为地球是个平面，所以得出的结果跟事实差距很大。但是如果把太阳换成一幢高楼、一座山峰或者一口深井，陈子的方法是可以得出正确答案的。更重要的是，陈子测日可以作为一个典型，说明勾股定理的起源，是来自于中国古人对于天文历法的探究。

中国是农耕文明发源地之一，自上古起，中国人顺应天时，开垦田园，把天时与农事互相结合，以期获得农作物的最大产量。通过观测天文，推算历法和设立节气，推动着中国农耕文明不断进步，也积极促进了数学的发展。蕴藏于天与地之中的各种“数”，就在古人的生活生产中被发现了。

从测量土地，到测量山河，再到测量宇宙；从伏羲造圭，到大禹治水，再到周公问数，夏华文明在不断的探索中发展。勾股定理，就是在这个历史文化进程中诞生的。